"Риск прогнозирования" может быть учтен в объемах закупки услуги или объеме подготовленной услуги (численность наемного штата специалистов) как прямая величина процента от объема продаж. То есть в нашем примере, рекомендуется запланировать на декабрь 2003 года продажи в объеме:

Q= QTREND* var=46,3*0.94=43.5 тыс. руб.

То есть рассчитанная величина риска снижает планируемый нами объем продаж.

2.2.Анализ тенденций развития предприятия.

Статистическое описание движения во времени экономических явлений осуществляется, как известно, с помощью динамических (временных) рядов. Уровни таких рядов формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и в том числе различного рода случайностей. Изменение условий развития явления приводит к более или менее интенсивной смене самих факторов, к изменению силы и результативности их воздействия и в конечном счете к вариации уровня изучаемого явления во времени. Лишь в очень редких случаях в экономике встречаются чисто стационарные ряды, т.е. ряды, динамика уровней которых такова, что средние характеристики не изменяются во времени. В таких случаях вариацию можно приписать действию только случайных причин и изучать ее с помощью теории стационарных случайных процессов. В западной статистической литературе уровень динамического ряда, характеризующего развитие экономического явления, традиционно рассматривается как сумма четырех компонент, которые непосредственно не могут быть измерены (ненаблюдаемые компоненты): вековой уровень (secular trend), или тренд, циклическая составляющая, сезонная составляющая и случайные колебания. Расчленение на вековой уровень и циклическую составляющую можно рассматривать лишь как технический прием при изучении циклов, если требуется измерить продолжительность отдельных этапов цикла. Несмотря на условность подобного расчленения уровней динамического ряда, этот прием можно применить для различного рода практических расчетов, главным образом для выделения тенденции развития, определения закономерности движения того или иного уровня во времени. Понятие тенденции развития не имеет достаточно четкого определения. В статистической литературе под тенденцией развития понимают некоторое общее направление развития, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории. Предполагается, что такая траектория, которую можно охарактеризовать в виде некоторой функции времени, назовем ее трендом, характеризует основную закономерность движения во времени и в некоторой мере (но не полностью) свободна от случайных воздействий. Тренд описывает фактическую усредненную для периода наблюдения тенденции изучаемого процесса во времени, его внешнее проявление. Результат при этом связывается исключительно с ходом времени. Предполагается , что через время можно выразить влияние всех основных факторов. Механизм их влияния в явном виде не учитывается. По существу, линия тренда выполняет ту же функцию для последовательных во времени наблюдений, что и средняя величина в ряде распределения. Часто под трендом понимают регрессию на время. Иногда тренд представляют как детерминированную компоненту переменной (причем не обязательно изменение этой компоненты связывают со временем). Каждое из подобных определений, скорее, указывает на частный прием отыскания тренда, а не на его сущность. Простые приемы анализа тенденций развития. Пожалуй, ни один вид статистических показателей, исключая разве что средние, не используется так часто в экономическом анализе, как средний темп роста. Средний темп роста можно получить как геометрическую среднюю из ряда последовательных (цепных) темпов роста. Цепной темп роста характеризует отношение какого-либо уровня динамического ряда к предыдущему уровню и выражается в процентах или в долях единицы. В последнем случае его называют коэффициентом роста. Если ряд состоит из уровней y1, y2, … yt, то цепные темпы роста (τt) будут равны:

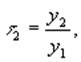
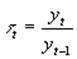… , . Соответственно цепные темпы прироста, выраженные в долях единицы . будут равны:

Если тенденция развития в известном временном интервале охарактеризована с помощью некоторого постоянного темпа роста, то в качестве последнего принимается средний темп за соответствующий период. Средний темп роста обычно определяют как

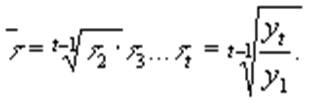(1.10) Нетрудно показать, что средний темп роста при дискретных показателях времени представляют собой знаменатель геометрической прогрессии, а средний темп прироста соответствует норме процента в формуле сложных процентов : Cn = C0 , где Сn, C0 - суммы на конец и начало периода; n=t-1 – число истекших лет; р- норма процента. Заменив в формуле сложных процентов Сn и С0 на yt и y1 соответственно, а на некоторый постоянный темп роста τ, получим:

yt =y1 ·τt-1 (1.11) Величина τt-1 соответствует показательной функции. Допустим теперь, что изменение ряда происходит непрерывно, тогда формула (1.11) будет характеризовать развитие по показательной или экспоненциальной кривой. Если исследуемый ряд непрерывен (такой ряд можно представить себе как результат наблюдений при бесконечном дроблении интервалов времени) и задан в виде дифференцируемой функции yt = ft, то мгновенный темп прироста определяется как

(1.12) где f`t -производная функции. Возьмем теперь экспоненциальную функцию , где е – основание натуральных логарифмов, a1 и a2 - параметры. Производная этой функции составит: , а исчисленный в соответствии с (1.12) темп прироста равен: Таким образом, экспоненциально зависящая от времени функция имеет постоянный темп прироста, равный значению ее параметра a2 . Напишем теперь выражение для экспоненциальной функции в виде

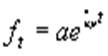(1.13) Рассмотрим теперь ряд вопросов, связанных с одновременным анализом нескольких динамических рядов, и прежде всего проблему соотношения темпов роста частей и целого. Пусть анализируется m динамических рядов, j = 1,…, m, причем сумма этих рядов дает новый ряд:

(1.14) Пусть динамика каждого ряда характеризуется цепными темпами роста τjt . Соответственно цепной темп роста суммарного ряда равен ρt. Уровни этих рядов на период t можно представить как уровни предшествующего периода, умноженные на соответствующие темпы роста: