Расчеты показателя внутренней нормы доходности по методике, речь о которой будет идти несколько ниже, дали следующие результаты: за квартал показатель составит 0,0698. В пересчете на год это величина будет соответствовать 27,95%.

Много это или мало, хорошо это или плохо — определяет сам инвестор, ибо данный показатель относится к разряду абсолютных оценок доходности проекта. Если инвестор решил, что такой доход за каждый квартал жизненного цикла проекта его вполне устраивает, то он будет такой проект реализовывать (при условии, что он единственный) или включит его в список для конкурсного отбора (если есть несколько альтернативных проектов).

Методически показатель внутренней нормы рассчитывается по формулам

(8.1)

или (8.2)

где Д i — доход предприятия в i -ом временном интервале:

Д i = J i (B i — C i ) (8.3 )

J i _ величина инфляционного коэффициента (формула 6.20) в i -ом временном интервале;

B i — выручка предприятия в i -м временном интервале;

C i — себестоимость продукции (без амортизационных отчислений ) в i -ом временном интервале;

K i — инвестиционные вложения в i -ом временном интервале, которые принимаются по проекту с учетом инфляции национальной валюты:

К i = Ф в i — R i , (8.4)

Ф в i — коэффициент инфляции национальной валюты за период от начала инвестирования до i -го временного интервала:

Ф в i = (1 + И i )( l + И 2 )(1 + И 3 ) .(1 + И п ) (8.5)

И 1 , И 2 , И 3 . И п — темпы инфляции национальной валюты в соответствующем временном интервале (в долях от единицы);

R i — инвестиционные платежи по проекту в i -ом временном интервале (без учета инфляции);

q — показатель внутренней нормы доходности за временной интервал в долях от единицы;

i — текущий временной интервал, принимающий значения от 0 до Т ;

Т — длительность жизненного цикла проекта, исчисляемая в принятых временных интервалах.

Произведем расчет (а точнее, проверку ранее полученного и приведенного) показателя внутренней нормы доходности по формуле 8.1.

Вначале определим суммарную величину дохода предприятия за весь жизненный цикл проекта (информацию для расчета возьмем из таблицы 8.1).

Теперь подсчитаем суммарные инвестиционные вложения.

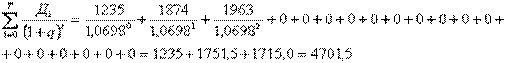
Таким образом, условие формулы 8.1 или 8.2 точно выдерживается. Суммарная величина дохода предприятия за весь жизненный цикл проекта, исчисленная с учетом фактора времени и приведенная к началу инвестирования, с высокой точностью соответствует суммарным инвестиционным вложениям (4701,5 = 4701,5). Это значит, что в данном конкретном проекте показатель внутренней нормы доходности действительно соответствует q = 0,0698.

Однако возникает вопрос о том, как же определить величину искомого показателя— Ведь определить ее напрямую по формулам 8.1 или 8.2 при достаточно большом количестве временных интервалов практически невозможно. Для этого обычно пользуются при расчетах внутренней нормы доходности компьютерными программами, позволяющими в считанные доли минуты определить искомую величину с достаточной точностью.

Разумеется, не всегда под рукой имеется компьютер, а к нему — не у всех есть соответствующая программа. И все же опытный расчетчик может вручную, с помощью обычного калькулятора произвести необходимые вычисления и определить показатель внутренней нормы доходности, затратив на эту процедуру около часа или несколько больше. Все зависит от того, как много временных интервалов будет использоваться в расчетах и с какой точностью надо получить решение поставленной задачи. При этом сама методика расчетных операций не очень обременительна. Она предполагает постепенное приближение получаемого результата к его окончательному виду в итерационном процессе, при котором с каждым последующим шагом все расчетные операции повторяются, производится коррекция величины показателя, и так до тех пор, пока искомый результат не будет получен.

Покажем на конкретном примере, как следует применять ручной счет внутренней нормы доходности и какими приемами надо при этом пользоваться. Для простоты описания воспользуемся проектом, условия которого представлены в табл. 8.1.

Итак, представим всю совокупность расчетных приемов в виде системы последовательных шагов.

Первый шаг. Определим простую сумму инвестиционных вложений и сумму доходов предприятия за весь жизненный цикл проекта. Первая величина составляет, судя по исходным данным, — К i = (1235 + 1874 + + 1963) = 5074 тыс. руб. Вторая величина определяется следующим образом:

— Д i = 0 + 0 + 0 + 502 + 520 + . + 600 + 600 = 9252 тыс. руб.

Простое сравнение двух полученных величин свидетельствует о том, что доходная составляющая больше инвестиционной (9252 > 5074). Наличие именно такого неравенства однозначно определяет внутреннюю норму доходности как величину больше нуля.

Если бы две сравниваемые величины точно совпали, то тогда искомый показатель был бы равен нулю. И наконец, в случае когда инвестиционная сумма больше доходной составляющей, искомый показатель внутренней нормы доходности представляет отрицательную величину. Но тогда инвестор, очевидно, откажется от такого проекта и примет к рассмотрению исследуемый проект лишь тогда, когда доходы предприятия будут больше инвестиций. Именно такой случай рассматривается в нашем примере. Поэтому можно перейти к дальнейшему анализу и определению величины внутренней нормы доходности.

Второй шаг. Устанавливают величину искомого показателя на определенном уровне. Предположим, что расчетчик примет показатель q = 0,1, после чего произведет расчеты инвестиционных вложений и доходной составляющей проекта с применением при нятой нормы доходности по формуле 8.2. Тогда у него получится отрицательная величина, ибо сумма инвестиций окажется больше доходной составляющей проекта (читатель может сам убедиться в этом, произведя соответствующие расчеты). Такой результат будет свидетельствовать о том, что установленная эмпирическим путем величина внутренней нормы доходности должна быть в данном проекте меньше 0,1 и, следовательно, дальнейший поиск связан с некоторым уменьшением величины этого показателя. Обычно если выполнять расчет чисто механически, то можно для дальнейших расчетов принять среднее значение показателя между двумя соседними расчетами, т.е. в нашем примере это будет q = 0,05, поскольку этот результат и есть средняя между 0 и 0,1.

Приняв новое значение внутренней нормы доходности, переходят к новому шагу в проводимых расчетах.

Третий шаг. Все расчеты точно повторяются, но уже с нормой доходности q = 0,05. Опять-таки возможны два случая: либо разность между доходной и инвестиционной частями проекта больше, либо она меньше нуля. Если имеет, место последний случай, то надо уменьшать внутреннюю норму доходности (например, до величины q = 0,025) и все расчеты повторить. Если окажется, что разность двух составляющих проекта будет положительной, т.е. больше нуля (именно так случится в нашем примере, если все расчеты произвести по аналогии с ранее выполняемыми), то значение принимаемой нормы доходности надо будет вновь увеличить, доведя ее до величины q = 0,075. Это значение будет достаточно близким к истинной величине искомой нормы доходности, которая была получена на уровне q = 0,0698 с помощью компьютерной технологии.