2

Содержание

Введение 3

2. Нахождение асимптоты 4

2.1 Геометрический смысл асимптоты 5

2.2 Общий метод нахождения асимптоты 6

3. Виды 8

3.1 Горизонтальная асимптота 8

3.2 Вертикальная асимптота 9

3.3 Наклонная асимптота 10

Использованная литература 12

3

Введение

Асимптота, так называемая прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает ее, так что расстояние между ними делается бесконечно малой величиной.

Понятие асимптоты играет важную роль в математическом анализе. Они проводятся при изучении свойств многих кривых (гиперболы, конхоиды, логарифмич. линии, циссоиды и др.).

4

2. Нахождение асимптоты

Пусть функция f (x) определена для всех x > а (соответственно для всех

x < а). Если существуют такие числа k и l, что f(x) - kx - l = 0 при х ® + ¥ (соответственно при х ® - ¥), то прямая

y = kx + l

называется асимптотой графика функции f (x) при x ® + ¥ (соответственно при х ® - ¥).

Существование асимптоты графика функции означает, что при х ® + ¥

(или х ® - ¥) функция ведёт себя «почти как линейная функция», то есть отличается от линейной функции на бесконечно малую.

x- 3x - 2

Найдём, например, асимптоту графика функции y = x +1

Разделив числитель на знаменатель по правилу деления многочленов,

2 2

получим y = x - 4 + x + 1 Так как x + 1 = 0 при х ® ± ¥, то прямая y = x-4

является асимптотой графика данной функции как при х ® + ¥,

так и при х ® - ¥.

5

2.1 Геометрический смысл асимптоты

Рассмотрим геометрический смысл асимптоты. Пусть М = (x, f (x)) – точка графика функции f, М - проекция этой точки на ось Ох, АВ – асимптота,

q - угол между асимптотой и положительным направлением оси Ох, q ¹,

MP – перпендикуляр, опущенный из точки М на асимптоту АВ, Q – точка пересечения прямой ММ с асимптотой АВ (рис.1).

(рис.1)

Тогда ММ = f (x), QM = kx + l, MQ = MM - QM = f (x) – (kx +l),

MP = MQ cos q. Таким образом, MP отличается от MQ лишь на не равный нулю множитель cos q, поэтому условия MQ ® 0 и MP ® 0 при х ® + ¥ (соответственно при х ® - ¥) эквивалентны, то есть lim MQ = 0,

то и lim MP = 0, и наоборот. х ® + ¥

х ® + ¥

Отсюда следует, что асимптота может быть определена как прямая, расстояние до которой от графика функции, то есть отрезок МР, стремится к нулю, когда точка М = (x, f (x)) «стремится, оставаясь на графике, в бесконечность» (при х ® + ¥ или, соответственно, х ® - ¥).

6

2.2 Общий метод отыскания асимптоты

Укажем теперь общий метод отыскания асимптоты, то есть способ определения коэффициентов k и l в уравнении y = kx + l.

Будем рассматривать для определённости лишь случай х ® + ¥ (при х ® - ¥ рассуждения проводятся аналогично). Пусть график функции f имеет асимптоту y = kx + l при х ® + ¥. Тогда, по определению,

f (x) = kx + l + 0

Разделим обе части равенства f (x) = kx + l + 0 на х и перейдём к пределу при х ® + ¥. Тогда

lim = k.

х ® + ¥

Используя найденное значение k, получим из f (x) = kx + l + 0 для определения l формулу

l = lim (f (x) – kx).

х ® + ¥

Справедливо и обратное утверждение: если существуют такие числа k и l, что выполняется условие l = lim (f (x) – kx), то прямая y = kx + l является

х ® + ¥

асимптотой графика функции f (x). В самом деле, из l = lim (f (x) – kx) имеем

х ® + ¥

lim [f (x) - (kx + l)] = 0,

х ® + ¥

то есть прямая y = kx + l действительно удовлетворяет определению асимптоты, иначе говоря, выполняется условие f (x) = kx + l + 0. Таким образом, формулы lim = k. и l = lim (f (x) – kx)

х ® + ¥ х ® + ¥

сводят задачу отыскания асимптот y = kx + l к вычислению пределов определённого вида. Более того, мы показали, что если существует

представление функции f в виде f (x) = kx + l + 0, то k и l выражаются по формулам lim = k. и l = lim (f (x) – kx)

х ® + ¥ х ® + ¥

Следовательно, если существует представление y = kx + l, то оно единственно.

Найдём по этому правилу асимптоту графика функции f (x) = ,

найденную нами выше другим способом:

7

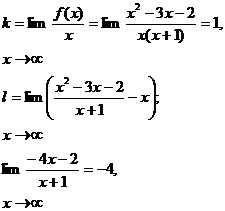
то есть мы, как и следовало ожидать, получили тоже уравнение асимптоты

y = x – 4, как при х ® + ¥, так и при х ® - ¥.

В виде y = kx + l может быть записано уравнение любой прямой, непараллельной оси Oy. Естественно распространить определение асимптоты и на прямые, параллельные оси Oy.

8

3. Виды

3.1 Горизонтальная асимптота

Пусть $ lim f (x) = b. Тогда говорят, что у функции f (x) имеется горизонтальная асимптота y = b. График функции чаще всего имеет такой вид (при x ® +¥) (рис.2)

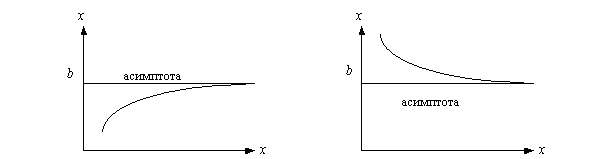хотя в принципе, может иметь и такой вид (рис.3)

(рис.3)

9

3.2 Вертикальная асимптота

(рис.4)

Пусть при x ® a ± 0 lim f (x) = ± ¥. Тогда говорят, что прямая x = a является