Широко применяют также еще один упругий параметр-коэффициент Пуассона ν, являющийся коэффициентом пропорциональности только между деформациями - относительными продольными ∆l/l и относительными поперечными ∆ d/d:

∆ d/d= ν·∆l/l

Коэффициент Пуассона - величина безразмерная. Он связан с величинами Е и G уравнением:

Для изотропных тел достаточно знать лишь два упругих параметра; другие параметры могут быть вычислены по соотношениям теории упругости.

Например,

Чаще всего в качестве основных параметров экспериментально определяют и используют в расчетах модуль упругости и коэффициент Пуассона.

Расчетная часть

q- напряжения нетронутого массива пород на бесконечности,

E,υ- модуль упругости и коэффициент Пуассона.

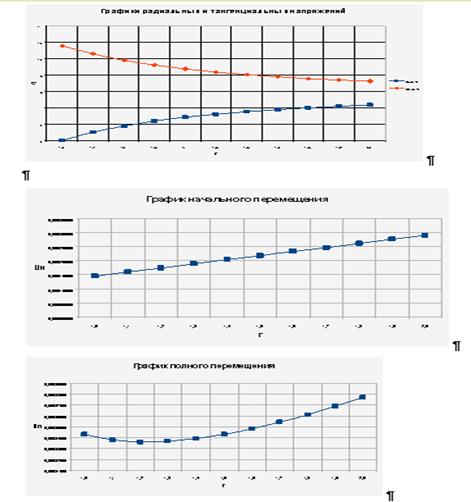
2. Распределение полных напряжений в массиве пород вокруг выработки описывается следующим образом

1) σr=q*(1-(1/r²))

σr1=5,8*(1-(1/1,02))= 0 Мпа

σr2=5,8*(1-(1/1,12))= 1.006 Мпа

σr3=5,8*(1-(1/1,22))= 1.772 Мпа

σr4=5,8*(1-(1/1,32))= 2.368 Мпа

σr5=5,8*(1-(1/1,402))= 2.841 Мпа

σr6=5,8*(1-(1/1,52))= 3.222 Мпа

σr7=5,8*(1-(1/1,62))= 3.534 Мпа

σr8=5,8*(1-(1/1,702))= 3.793 Мпа

σr9=5,8*(1-(1/1,82))= 4.009 Мпа

σr10=5,8*(1-(1/1,92))= 4.193 Мпа

σr11=5,8*(1-(1/2,02))= 4.35 Мпа ,

где σr-радиальное напряжение, r-радиальная координата.

2) σθ= q*(1+(1/r²))

σθ1=5,8*(1+(1/1,02))= 11.6 Мпа

σθ2=5,8*(1+(1/1,12))= 10.593 Мпа

σθ3=5,8*(1+(1/1,22))= 9.827 Мпа

σθ4=5,8*(1+(1/1,32))= 9.231 Мпа

σθ5=5,8*(1+(1/1,42))= 8.759 Мпа

σθ6=5,8*(1+(1/1,52))= 8.377 Мпа

σθ7=5,8*(1+(1/1,62))= 8.065 Мпа

σθ8=5,8*(1+(1/1,72))= 7.806 Мпа

σθ9=5,8*(1+(1/1,82))= 7.590 Мпа

σθ10=5,8*(1+(1/1,92))= 7.406 Мпа

σθ11=5,8*(1+(1/2.02))= 7.25 Мпа ,

где σθ-тангенциальное напряжение , r-радиальная координата

3. Находим полные радиальные перемещения

Un= q/E*((1- υ)*r+(1+ υ)/r)

U0= q/E*(1- υ)*r,

U= q*(1+ υ)/E*r

- U0-начальное радиальное перемещение

- Un-полные радиальные перемещения

- U-дополнительные радиальные перемещения

1) U0= q/E*(1- υ)*r

U01= (5.8/3.2*104)*(1-0.2)*1.0= 0.00014

U02= (5.8/3.2*104)*(1-0.2)*1.1= 0.00015

U03= (5.8/3.2*104)*(1-0.2)*1.2= 0.00017

U04= (5.8/3.2*104)*(1-0.2)*1.3= 0.00018

U05= (5.8/3.2*104)*(1-0.2)*1.4= 0.00020

U06= (5.8/3.2*104)*(1-0.2)*1.5= 0.00021

U07= (5.8/3.2*104)*(1-0.2)*1.6= 0.00023

U08= (5.8/3.2*104)*(1-0.2)*1.7= 0.00024

U09= (5.8/3.2*104)*(1-0.2)*1.8= 0.00026

U10= (5.8/3.2*104)*(1-0.2)*1.9= 0.00027

U11= (5.8/3.2*104)*(1-0.2)*2.0= 0.00029

2) Un= q/E*((1- υ)*r+(1+ υ)/r)

Un1= (5.8/3.2*104)*((1-0.2)*1.0+1.2/1.0) = 0.000342

Un2= (5.8/3.2*104)*((1-0.2)*1.1+1.2/1.1) = 0.000337

Un3=(5.8/3.2*104)*((1-0.2)*1.2+1.2/1.2) = 0.000336

Un4=(5.8/3.2*104)*((1-0.2)*1.3+1.2/1.3) = 0.000336

Un5=(5.8/3.2*104)*((1-0.2)*1.4+1.2/1.4) = 0.000338

Un6=(5.8/3.2*104)*((1-0.2)*1.5+1.2/1.5) = 0.000342

Un7=(5.8/3.2*104)*((1-0.2)*1.6+1.2/1.6) = 0.000348

Un8=(5.8/3.2*104)*((1-0.2)*1.7+1.2/1.7) = 0.000354

Un9=(5.8/3.2*104)*((1-0.2)*1.8+1.2/1.8) = 0.000361

Un10=(5.8/3.2*104)*((1-0.2)*1.9+1.2/1.9) = 0.000368

Un11=(5.8/3.2*104)*((1-0.2)*2.0+1.2/2.0) = 0.000377

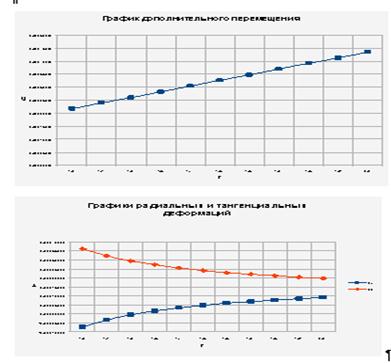
3) U= q*(1+ υ)/E*r

U1= 5.8*1.2/ 3.2*104*1.0 = 0.000217

U2= 5.8*1.2/ 3.2*104*1.1 = 0.000239

U3= 5.8*1.2/ 3.2*104*1.2 = 0.000261

U4= 5.8*1.2/ 3.2*104*1.3 = 0.000282

U5= 5.8*1.2/ 3.2*104*1.4 = 0.000304

U6= 5.8*1.2/ 3.2*104*1.5 = 0.000326

U7= 5.8*1.2/ 3.2*104*1.6 = 0.000348

U8= 5.8*1.2/ 3.2*104*1.7 = 0.000369

U9= 5.8*1.2/ 3.2*104*1.8 = 0.000391

U10= 5.8*1.2/ 3.2*104*1.9 = 0.000413

U11= 5.8*1.2/ 3.2*104*2.0 = 0.000435

6. Определяем радиальные и тангенциальные деформации εθ, εr

εθ =(1/E)*(σθ-0.2*σr)

εr=(1/E)*(σr -0.2*σθ)

1) εθ =(1/E)*(σθ-0.2*σr)

εθ1 = (1/3.2*104)*(11.6-0,2*0.000)= 0.000362

εθ2 = (1/3.2*104)*(10.593-0,2*1.006)= 0.000324

εθ3 = (1/3.2*104)*(9.827-0,2*1.772)= 0.000296

εθ4 = (1/3.2*104)*(9.231-0,2*2.368)= 0.000273

εθ5 = (1/3.2*104)*(8.759-0,2*2.840)= 0.000255

εθ6 = (1/3.2*104)*(8.377-0,2*3.222)= 0.000241

εθ7 = (1/3.2*104)*(8.065-0,2*3.534)= 0.000229

εθ8 = (1/3.2*104)*(7.806-0,2*3.793)= 0.000220

εθ9 = (1/3.2*104)*(7.590-0,2*4.009)= 0.000212

εθ10 = (1/3.2*104)*(7.406-0,2*4.193)= 0.000205

εθ11 = (1/3.2*104)*(7.25-0,2*4.35)= 0.000199

2) εr=(1/E)*(σr -0.2*σθ)

εr1= (1/3.2*104)*(0.000-0,2*11.6)= -0.000072

εr2= (1/3.2*104)*(1.006-0,2*10.593)= -0.000034

εr3= (1/3.2*104)*(1.772-0,2*9.827)= -0.000006

εr4= (1/3.2*104)*(2.368-0,2*9.231)= 0.000016

εr5= (1/3.2*104)*(2.840-0,2*8.759)= 0.000034

εr6= (1/3.2*104)*(3.222-0,2*8.377)= 0.000048

εr7= (1/3.2*104)*(3.534-0,2*8.065)= 0.000060

εr8= (1/3.2*104)*(3.793-0,2*7.806)= 0.000069

εr9= (1/3.2*104)*(4.009-0,2*7.590)= 0.000077

εr10= (1/3.2*104)*(4.193-0,2*7.406)= 0.000084

εr11= (1/3.2*104)*(4.35-0,2*7.25)= 0.000090

Заключение

1. Овладел методами решения указанной задачи в полном объёме (метод сил и метод перемещений).

2. Исходя из методов результатов решения, можно заключить, что радиальное напряжение σr имеет прямо пропорциональную зависимость от радиальной координаты r, а тангенциальное напряжение σθ имеет обратно пропорциональную зависимость от r.

Список используемой литературы:

1. Баклашов И.В., Картозия Б.А. Механика подземных сооружений и конструкций крепей. М., 1984. 415 с.

2. Борисов А.А. Механика горных пород и массивов. М., Недра, 1980. 360 с.

3. Булычев Н.С. Механика подземных сооружений. М., Недра, 1982. 272 с.

4. Напряженно-деформированное состояние мерзлого массива пород вокруг вертикального ствола (методические указания)// Составитель Иудин М.М. Якутск, ЯГУ, 1997. 26 с.