;

;

отсюда

.

3. Построение диаграммы Максвелла - Кремоны

Диаграмма Максвелла - Кремоны начинается с построения верёвочного многоугольника внешних сил. Для начала определяют внешние и внутренние поля фермы. Внешние поля фермы обозначаются заглавными буквами латинского алфавита, внутренние - строчными. Внешние поля ограничены линиями действия внешних нагрузок, опорных реакций и стержнями, помещёнными на внешнем контуре фермы. Внутри поля ограничиваются только стержнями фермы и лежат внутри контура фермы (рис.6).

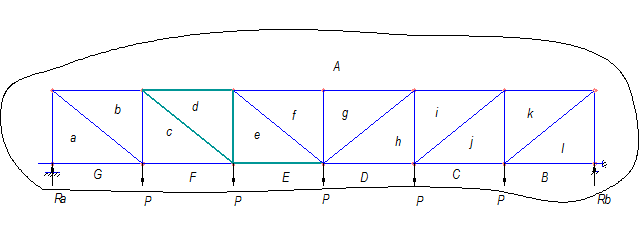Рис. 6

Поля на диаграмме Максвелла - Кремоны обозначаются точками. Выбираем два поля на схеме, разделённых опорной реакцией.

Выбираем масштабный коэффициент:

.

На диаграмме опорные реакции и внешние усилия, а так же внутренние усилия стержней обозначаются отрезками.

Неизвестные точки, обозначающие внутренние поля, находятся в пересечении двух линий, на которых будут обозначаться отрезками усилия, лежащие между уже известными внешними (внутренними) полями (рис.7).

Рис.7

4. Построение линий влияния усилий в стержнях фермы

Линии влияния используются для расчетов ферм, на которые действует подвижная нагрузка.

Линия влияния представляет собой диаграмму, при построении которой функцией является изучаемая величина усилия, а независимой переменной -абсцисса груза (его местоположение на оси абсцисс). Каждая ордината линии влияния численно равна значению изучаемого усилия для положения силы на сооружении над этой ординатой.

Для построения любой линии влияния в данном месте сооружения применяют следующий статический метод. Поставив груз в произвольное положение, определяемое абсциссой , и применяя условие равновесия, даем аналитическое выражение данного усилия, затем, изменяя, даем это выражение в графической форме.

Строим линии влияния для реакций опор:

Рис.8

Для реакции опоры составляем уравнение моментов относительно точки :

;

;

отсюда

;

при x=0; RA=1;

при x=6d; RA=0.

Аналогично для реакции опоры составляем уравнение моментов относительно точки А:

;

;

отсюда

;

при x=0; RВ=1;

при x=6d; RВ=0.

Для построения линии влияния усилия в стержне рассечём ферму на две части по пролёту, в котором находится искомый стержень, и будем рассматривать левую и правую части фермы при отсутствии на них подвижной нагрузки.

Находим усилие в стержне DF и DG для чего рассматриваем сечение I - I (см. рис. 2):

Слева:

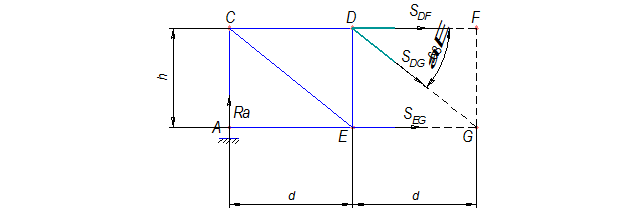Рис.9

Составляем уравнение моментов относительно точки (рис. 9):

;

;

отсюда

Составляем уравнение суммы проекций всех сил на ось (рис. 9):

;

отсюда

Справа:

Рис.10

Составляем уравнение моментов относительно точки (рис.10):

;

;

отсюда

Находим усилия в стержнях FG и GI, для чего рассматриваем сечение II - II (см. рис. 2):

Слева:

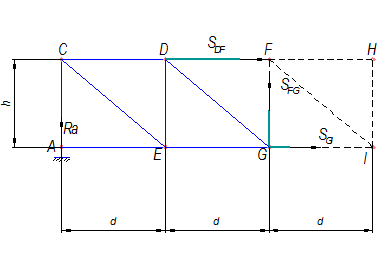
Рис.11

Составляем уравнение моментов относительно точки (рис. 11):

;

отсюда

Составляем уравнение суммы проекций всех сил на ось (рис. 11):

;

;

отсюда