Олигополия
Первая фирма может исходить из следующих рассуждений. Если она снизит цену, то ее прибыль возрастет с 8 до 10, а прибыль ее конкурента снизится до 3. Однако разумно предположить, что и вторая фирма в этом случае снизит цену, чтобы повысить свою прибыль до 5. Таким образом, ожидая в ответ на понижение цены на свою продукцию того же от конкурента, дуополист не будет переходить от средней цены к низкой.
Перейти от средней цены к высокой первой фирме есть смысл только в том случае, если вторая последует за ней. Последует ли она? При сохранении средней цены на свою продукцию вторая фирма получит 13 ден. ед. прибыли, а при переходе к высокой — только 10. Следовательно, первая фирма ожидает, что при переходе от средней цены к высокой ее конкурент сохранит среднюю цену. Результаты проведенного первой фирмой анализа в области ценовой политики таковы: если она снизит цену на свою продукцию, то же сделает и конкурент, и прибыли уменьшатся; если она повысит цену, то конкурент не последует за ней, и ее прибыль сократится в еще большей мере.
К такому же выводу на основе аналогичных рассуждений может прийти вторая фирма, и на рынке установится равновесие при средних ценах.
|
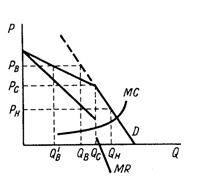
Рис. 2. Кривая спроса олигополиста. |
Вывод, к которому пришли конкуренты на основе проведенных рассуждений, можно представить графически в виде ломаной кривой спроса на их продукцию (рис. 2).
Придерживаясь средней цены Рс, фирма реализует Qc ед. продукции. Поскольку при повышении цены на ее продукцию конкурент не станет повышать цену на свою, то объем продаж данной фирмы сократится не до Qв, а до QB’ вследствие ухода части покупателей к конкуренту. Если фирма перейдет от средней цены к низкой, то конкурент тоже снизит цену на свою продукцию, и в результате каждая фирма сохранит свой контингент покупателей. Изгибу кривой спроса соответствует разрыв кривой предельной выручки, и когда точка Курно оказывается в этом разрыве, тогда изменение предельных затрат производства не вызывает изменения цены. Этим объясняется устойчивость цен на олигопольном рынке.
Хотя в рассматриваемом примере поведение дуополистов, приведшее к равновесию при средних ценах, не соответствует предпосылкам Курно, установившееся равновесие тождественно равновесию Курно: ни одна из фирм не заинтересована изменять цену на свою продукцию, пока ее конкурент не меняет цену на свою. В теории игр рассмотренная модель поведения игроков известна под названием “дилемма заключенного”.[1] В ней предполагается, что принятое решение конкурент не может “повернуть вспять”. В нашем примере это означает, что, после того как фирма перешла от средних цен к высоким, она уже не может вернуться к средним. Если это искусственное ограничение на поведение дуополистов снять, то рыночное равновесие в рассматриваемом примере может установиться и при высоких ценах на продукцию обеих фирм.
Вернемся к вопросу о том, последует ли вторая фирма за первой, когда последняя повысит цену. Если вторая фирма примет во внимание, что конкурент в случае сохранения ее цены на среднем уровне может вернуться к средней цене, то она скорей всего тоже поднимет цену на свою продукцию, так как при совместном повышении цен у обеих фирм прибыль возрастет с 8 до 10.
Таким образом, на рынке олигополии без явного сговора между конкурентами равновесие может установиться при цене, соответствующей монопольной. Однако такой результат тем менее вероятен, чем больше конкурентов действует в отрасли. С ростом числа конкурентов увеличивается вероятность того, что кто-то ради достижения временных выгод снизит цену на свою продукцию, подрывая сложившееся рыночное равновесие.
1.5. Ценообразование за лидером
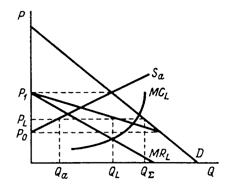
Одной из форм неявного соглашения конкурентов придерживаться единой цены на рынке гомогенного блага является ценообразование за лидером. В отличие от модели Штакельберга в данном случае лидер устанавливает не объем своего выпуска, а цену на свою продукцию. В качестве лидера выступает доминирующая по объему производства фирма, имеющая, как правило, более низкие средние затраты, чем аутсайдеры. Лидер устанавливает цену, максимизирующую его прибыль, а все другие фирмы — аутсайдеры воспринимают цену лидера в качестве экзогенного параметра. Аутсайдеры тем самым оказываются в положении конкурентной фирмы, кривая предложения которой совпадает с восходящим участком кривой предельных. Поэтому лидер, выбирая цену, знает, какой объем продукции предложат аутсайдеры по установленной им цене. Следовательно, для определения спроса на свою продукцию лидеру нужно из рыночного спроса вычесть предложение аутсайдеров. В графическом виде лидером изображен на рис.3. Кривая спроса, которая предстает перед лидером, образуется в результате горизонтального вычитания кривой совокупного предложения аутсайдеров Sa из кривой отраслевого спроса D: при Р >= P1 аутсайдеры удовлетворят рыночный спрос без лидера, а при Р < Р0 аутсайдеры уйдут с рынка, оставляя весь спрос лидеру. Точка пересечения кривых
|
Рис. .3 Ценообразование за лидером на рынке гомогенного блага |
предельной выручки и предельных затрат лидера определяет цену pl, которая установится на данном рынке. По этой цене аутсайдеры предложат Qa, а лидер —ql ед. продукции. По построению qa + qb = Qå , т.е. pl является равновесной ценой.
Для алгебраического представления ценообразования за лидером примем, что отраслевой спрос характеризуется формулой Q^D = а - bР, функция общих затрат всех аутсайдеров имеет вид ТСA = 0.25QA^2, а лидера — ТСl = k + lql, где qa,ql соответственно выпуск аутсайдеров и лидера.
Аутсайдеры определяют объем своего предложения из равенства Р = МСa, т.е. Р = 0.5QA. Следовательно, их функция предложения имеет вид QA^S = 2Р. Тогда функция спроса на продукцию лидера представляется формулой QL^D = q^d -QA^S = a - bP - 2Р = a - P(b + 2). Соответственно функция цены спроса на продукцию лидера имеет вид Р = (a - QL)/(b + 2). Следовательно, общая выручка лидера определяется по формуле TRL = (аQL - QL^2)/(b+2), а предельная выручка — MRL = (a - 2QL)/(b + 2). Из равенства mrl = МСL определяется объем выпуска лидера:
(a - 2QL) / (b + 2) = lÞQL = (a - (b + 2)l) / 2.
Подставив этот объем выпуска в уравнение цены спроса на продукцию лидера, найдем равновесную цену:
P* = (a + (b + 2) l) / (2(b + 2)) = a / (4 + 2b) + l / 2.